寻找无向图中的割点(边)-Tarjan 算法
date
Jan 30, 2022
slug
图算法在表格行恢复中的应用
status
Published
tags
Algorithm
Graph
OCR
summary
图算法在表格行恢复中的应用
type
Post
问题定义
在无向连通图中,如果删除某个顶点后,图不再连通,则称这样的顶点为割点(Articulation Points or Cut Vertices)。如果在连通图上至少删掉 k 个顶点才能破坏图的连通性,则称改连通图的连通度为 k。下面是几个带有割点的图的示例:
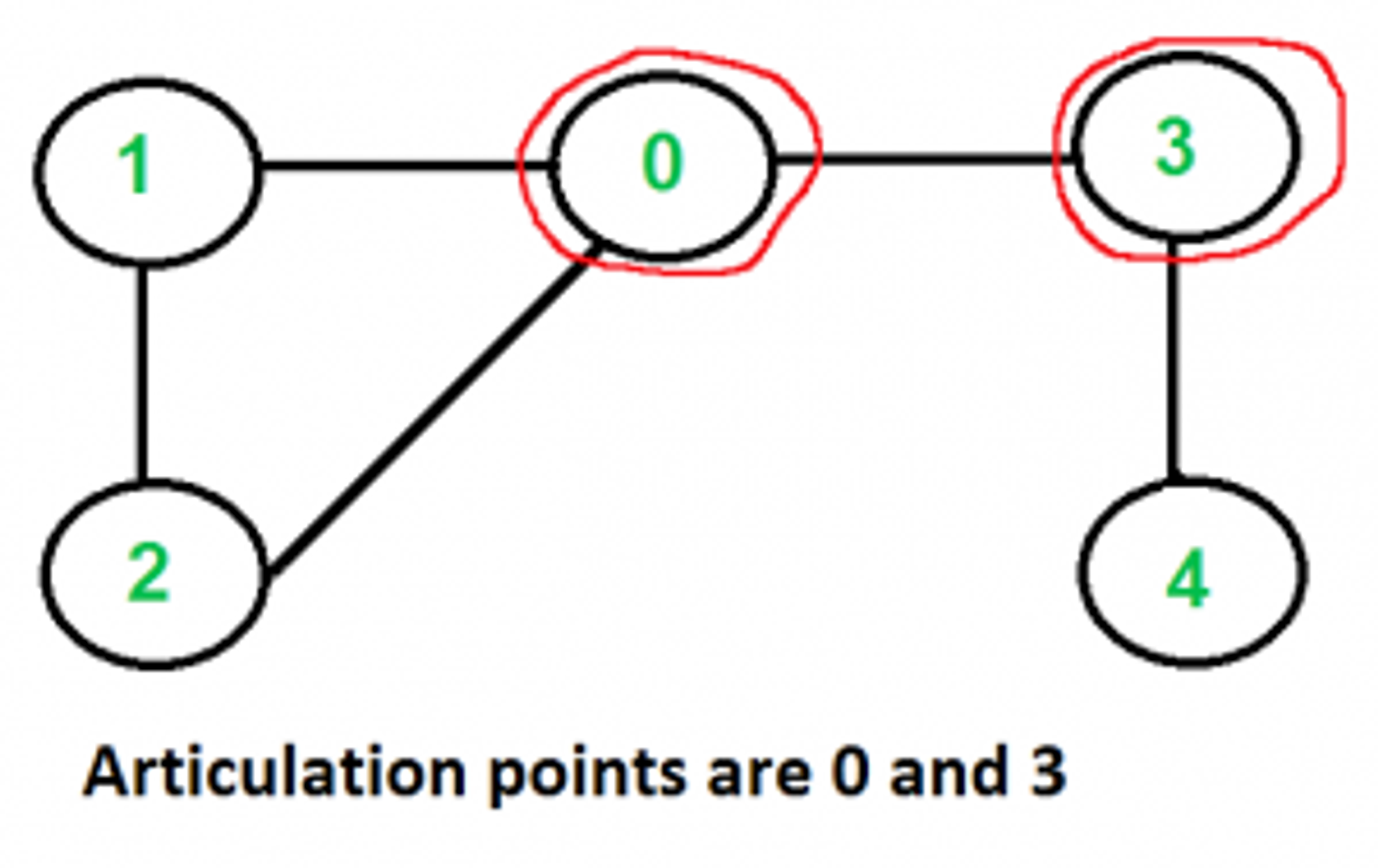
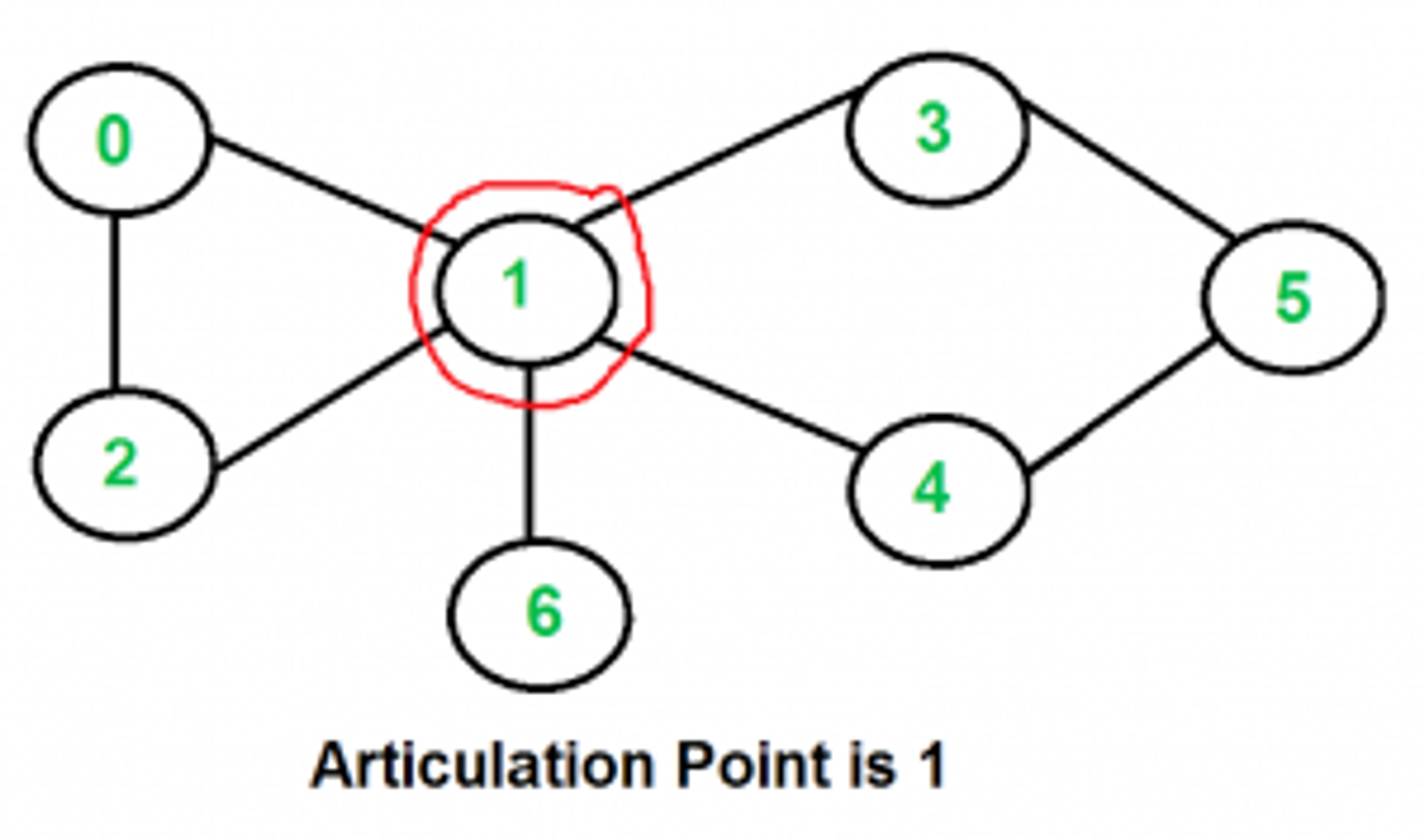
暴力算法
最暴力的方法是一次移除连通图中的节点,判断移除后的图是否连通。对每一个节点的操作流程如下:
- 从连通图中移除节点 u
- 判断剩下的节点之间是否相连(用 BFS 或者 DFS 遍历)
- 把 v 加回到连通图中
假设一个连通图有 V 个节点,E 条边,并且使用 adjacency list 来表示连通图,则时间复杂度为
Tarjan 算法
在 DFS tree 中判断一个节点 u 是否是割点,可以通过以下两个条件判断:
- u 是根节点,并且有至少两个子节点,则 u 是一个割点
- u 不是根节点,以 u 为分界,图可以分为两部分,一部分是已经访问过的节点,一部分是没有被访问过的节点,在没有被访问过的节点中至少有一个点在不经过 u 的情况下,无法回到已经访问过的点
- 叶子节点肯定不是割点
条件 1 很好判断,对于判断条件 2,我们需要维护两个数组,一个用来保存每个节点被遍历到的次序,记为
disc ,另一个保存所有节点,在不通过父节点的情况下能够访问到的最早的节点次序,记该数组为 low ,那么如果满足 low[v] >= disc[u] (v 最早只能访问到在 u 之后被访问到的节点)则说明节点 u 为割点。该条件如果把 = 号去掉,即可用来判断割边,因为 low[v] > disc[u] 时,表示 v 无法回到 u,此时 (u,v) 即表示一条割边,注意割边的判断无需要关心 u 是否为根节点。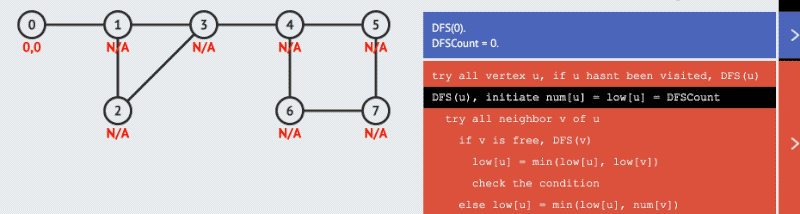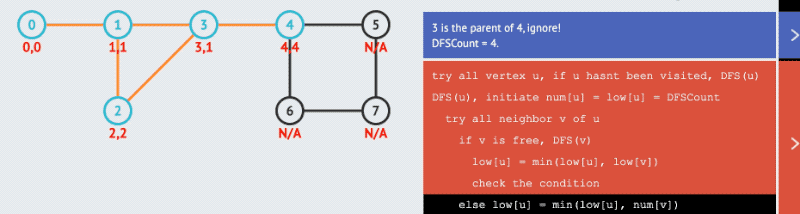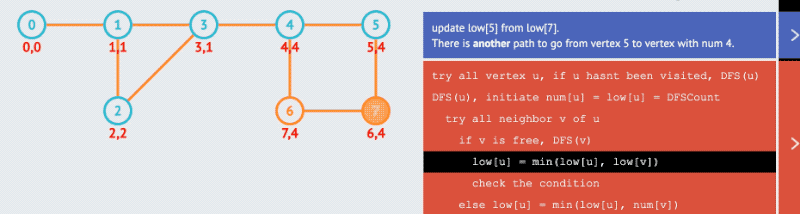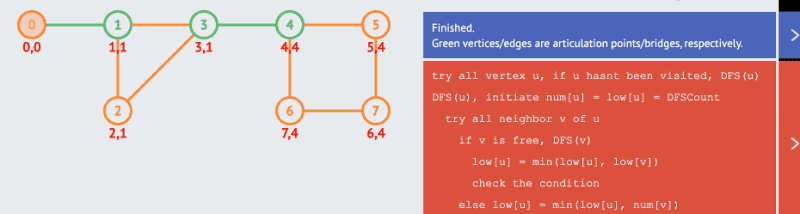
实际应用-表格行结构恢复
在表格行恢复问题中,需要判断两个文本框是否为同一行,相当于对所有两两组合的文本框关系进行二分类,这部分的网络结合了 LayoutXLM 和 StrucText 的关系分支,以后有机会可以再单独写一篇。
测试中发现,即使模型预测的 f1 很高,但还是免不了会出现某一行的某个节点和其它行的某个节点有关系,导致两行被合并,如下图,第一行和第二行合并了,第四行和第五行合并了。

以下为使用了 Tarjan 算法后的效果,每一行都明确的分开了。

参考:


